Solution:
Given the graphs of
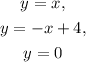
to be as plotted below:
The region ABC is bounded as shown above.
To find its area, the region ABC takes the shape of a triangle. Thus, we are to evaluate the area of the triangle ABC.
Step 1: Evaluate the midpoint between the distance AB.
The midpoint (x,y) of the distance AB is evaluated as
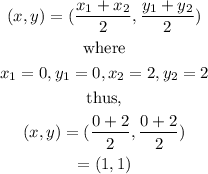
Thus, the midpoint of the distance AB is (1,1).
Step 2: Evaluate the height of the region (triangle).
The height of the region is the same as the distance between points A and the midpoint of the distance AB.
Thus,
The distance is evaluated as
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ x_1=2,y_1=2,x_2=1,y_2=1 \\ \text{thus,} \\ d=\sqrt[]{(1_{}-2_{})^2+(1_{}-2_{})^2} \\ =\sqrt[]{(-1_{})^2+(-1_{})^2} \\ =\sqrt[]{1+1} \\ d=\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fqd10cq2e4szqccmbwe12yz128yv8vdt6q.png)
Step 3: Evaluate the distance between points B and C.
The distance is evaluated similarly as
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ x_1=0,y_1=0,x_2=4,y_2=0 \\ \text{thus,} \\ d=\sqrt[]{(4_{}-0_{})^2+(0_{}-0_{})^2} \\ =\sqrt[]{4^2+0^2} \\ d=4\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7nxik5666l18n73xbe4rkv0po2pm7fpap7.png)
Step 4: Evaluate the area of the triangle ABC.
Given that the distance BC is 4 units and the height of the region is √2 units, the area of the region ABC is evaluated as the area of the triangle ABC.
Thus,
![\begin{gathered} \text{Area = }(1)/(2)*4*\sqrt[]{2} \\ \Rightarrow Area\text{ =2}\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/io1xd7o78jtg0nim8dsg8eqh7hy2ptrof3.png)
Hence, the area of the region is
![2\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/k0mps5f0tog0w5nhu416lrrm8ypia8rqp8.png)
The fourth option is the correct answer.