I need to know the new equation, I’ve provided a picture

Question

asked Jul 22, 2023 45.6k views

1 Answer

Alik Rokar · Answer 1 · 2023-07-27T01:01:52+0000

Hello there. To solve this question, we'll simply have to make x => x + 5 in the function.

Given the function:

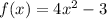
$f(x)=4x^2-3^{}$

We have to determine f(x + 5)

By making x => x + 5 in this function, we get:

$f(x+5)=4\cdot(x+5)^2-3$

Now remember the binomial expansion of order 2:

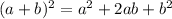
Therefore we have:

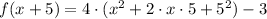
$f(x+5)=4\cdot(x^2+2\cdot x\cdot5+5^2)-3$

Multiply the terms inside parentheses and calculate the square.

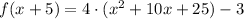
$f(x+5)=4\cdot(x^2_{}+10x+25)-3$

Apply the distributive property

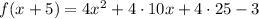
$f(x+5)=4x^2+4\cdot10x+4\cdot25-3$

Multiply and add the numbers

$\begin{gathered} f(x+5)=4x^2+40x+100-3 \\ \boxed{f(x+5)=4x^2+40x+97} \end{gathered}$

This is the answer we're looking for.

A way of showing this is the correct answer is to make x = 1 and x = 6 in the former function:

$\begin{gathered} f(1)=4\cdot1^2-3=4\cdot1-3=4-3=1 \\ f(6)=4\cdot6^2-3=4\cdot36-3=144-3=141 \end{gathered}$

Then making x = 1 in the expression we found after:

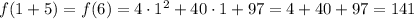
$f(1+5)=f(6)=4\cdot1^2+40\cdot1+97=4+40+97=141$

As expected.