Question

Use your answers from #1 and #2 to find the length of each arc between gondola cars. Use 3.14 for pi and round to the nearest hundredth. You must write out all the numbers you are multiplying together, meaning, show your work for full credit.

Answer 1

We have a SkyWheel.

We know that the angle between the gondolas is 360/41 = 8.78°.

The radius of the wheel is 181/2 = 90.5.

We know have to calculate the length of the arc between gondolas.

The length of the arc L can be calculated using proportions: the length of the arc is to the angle between gondolas as the total circumference of the wheel is to 2*pi (or 360°).

We can express this as:

`(L)/(\theta)=(C)/(2\pi)`

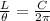
If we rearrange, we can solve for L:

`\begin{gathered} (L)/(\theta)=(C)/(2\pi) \\ (L)/(\theta)=(2\pi r)/(2\pi) \\ (L)/(\theta)=r \\ L=\theta\cdot r=((2\pi)/(41))\cdot90.5=((2\cdot3.14)/(41))\cdot90.5=13.86ft \end{gathered}`

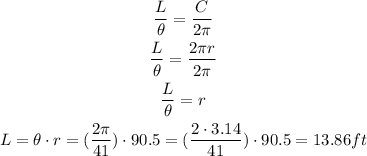
NOTE: we have to express the angle theta (that is the angle between the gondolas) in radians when we want to calculate a length. That is why this angle is expressed as the total angle of the circle (2*pi) divided the 41 gondolas.

If we use 8.78°, we should express it as:

`L=\theta\cdot r=8.78\degree\cdot((2\pi)/(360\degree))\cdot90.5ft=13.86ft`

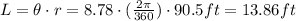
With the factor 2pi/360 we are converting the angle in degrees into radians in order to calculate the length.

Answer: the length of the arc between gondolas is 13.86 ft.