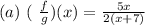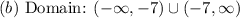Given the functions:
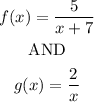
Let's solve for the following:
• (a) f/g
To solve for f/g let's divide f(x) by g(x).
We have:
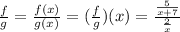
Solving further, we have:

Therefore, the function f/g is:
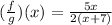
• (b) Domain of f/g.
The domain is the set of all possible x-values where the function is defined.
To find the domain, set the denominator to zero and solve for x.
We have:
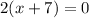
Divide both sides by 2:
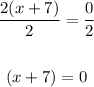
Subtract 7 from both sides:
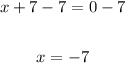
Therefore, the domian is:
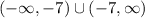
ANSWER: