The calculated value of the numerical expression
 is a. cube root of 4
is a. cube root of 4
How to evaluate the numerical expression
From the question, we have the following parameters that can be used in our computation:
the quantity 2 to the power of five sixths end quantity over the quantity 2 to the power of one sixth end quantity.
This means that

Applying the law of indices, we have
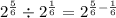
So, we have

Simplify
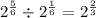
This can be further expressed as
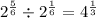
![2^\frac56 / 2^\frac16 = \sqrt[3]{4}](https://img.qammunity.org/2023/formulas/mathematics/high-school/k0cpt6736mg21dvne01bffczr482yqpir5.png)
Hence, the numerical expression is cube root of 4