Question

What is the area of the portion of the triangle that lies outside of the circle but within the triangle? Provide the answer along with an explanation of how to calculate the answer.

Answer 1

Step-by-step explanation:

Given:

To determine the area of the portion of the triangle that lies outside of the circle but within the triangle, we find the areas of triangle and circle first:

For the triangle, we use the formula:

A=1/2bh

where:

b=base

h=height

We plug in what we know:

`\begin{gathered} A=(1)/(2)bh \\ =(1)/(2)(20ft)(20ft) \\ =(1)/(2)(400ft^2) \\ \text{Calculate} \\ A=200ft^2 \end{gathered}`

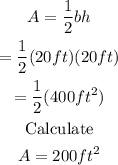
Next, we solve for the area of the circle using the given formula:

A=πr^2

where:

r=radius

So,

`\begin{gathered} A=\pi r^2 \\ =\pi(6ft)^2 \\ \text{Calculate} \\ A=113.1ft^2 \end{gathered}`

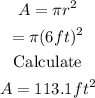
Then, to find the area of the portion of the triangle that lies outside of the circle but within the triangle:

Area of the portion = Area of the Triangle - Area of the Circle

We plug in what we know:

`\begin{gathered} \text{ }=200ft^2-113.1ft^2 \\ \text{Area of the portion = }86.9ft^2 \end{gathered}`

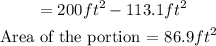
Therefore, the answer is 86.9 ft^2.