Question

I need to determine the length in feet of arc BC?? Is my answer correct?

Answer 1

l= π/2

1) To find out the length of the arc BC with a central angle ∠BAC, we'll use the following formula:

`l=(\alpha)/(360)\cdot2\pi r`

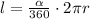
2) Now we can plug into that the given data, considering that ∠ BAC is a central angle then we can affirm:

`m\widehat{BC}=m\angle BAC`

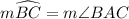
So we can plug into the formula below 45º as the angle of that arc, as it follows:

`\begin{gathered} l=(\alpha)/(360)\cdot2\pi r \\ l=(45)/(360)\cdot2\pi\cdot2 \\ l=(1)/(2)\pi\text{ or }(\pi)/(2) \end{gathered}`

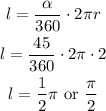
3) Hence, as we can see the answer is the l= π/2