In order to calculate the inside diameter, we can use the following relation, since the volumetric flow is constant for any part of the tube:
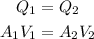
Where A is the cross-section area and V is the velocity.
Using V1 = 1.5 m/s, A1 = π*1.1²/4 and V2 = 10 m/s, we have:
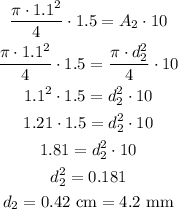
Therefore the correct option is the first one.