Question

Can you show me how to solve this and graph?

Answer 1

The points (x,y) whose values satisfy the equation -5y=13 belong to the graph of that equation.

First, isolate y by dividing both sides of the equation by -5 and simplifying:

`\begin{gathered} -5y=13 \\ \Rightarrow(-5y)/(-5)=(13)/(-5) \\ \Rightarrow y=-(13)/(5) \end{gathered}`

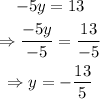
Then, the points (x,y) belon to the graph of the equation -5y=13 whenever the value of y is -13/5, regardless of the value of x. Then, choose two different values of x to find two points that belong to the graph. For example, x=0 and x=2. Then, this two points belong to the graph:

`\begin{gathered} (0,-(13)/(5)) \\ (2,-(13)/(5)) \end{gathered}`

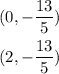
Notice that -13/5=-2.6,

Plot the points (0,-2.6) and (2,-2.6) in a coordinate plane:

Since the given equation is linear, the graph of the equation is a straight line. We can draw a straight line between any two points given. Draw a line between (0,-2.6) and (2,-2.6) to find the graph of the equation -5y=13: