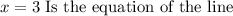Question

Find the equation of the line containing the given points. Write the equation in slope-intercept form. (3,8) and (3,-4)

Answer 1

Answer with explanation: We have to find the equation of the line that passes through the given coordinate points, (3,8) (3,-4) the general equation of the line is as follows:

`\begin{gathered} y(x)=mx+b\rightarrow(1) \\ m=(\Delta y)/(\Delta x)\rightarrow\text{ Slope of the equation} \end{gathered}`

The slope of the equation is calculated as follows:

`\begin{gathered} P_1(x_1,y_1)=(3,8) \\ P_2(x_2,y_2)=(3,-4) \\ \therefore\rightarrow \\ m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(-4-8)/(3-3)=\infty \\ m=\propto \end{gathered}`

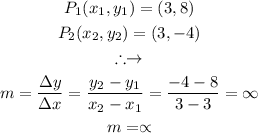
This suggests the equation of the line is simply a vertical line at x = 3, the graph of the equation is as follows:

`x=3\text{ Is the equation of the line}`