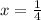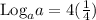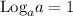Question

Write logaa=4x in exponential form and find x to evaluate logaa for any a>0, a≠1.

Answer 1

Given:

`\log _aa=4x`

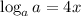
To find the exponential form of the above, all we need to do is to raise the base a to the power of 4x.

That is;

`a^(4x)=a`

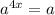
To find the value of x, we need to raise the power of the right - hand side so that we can equate the exponent

That is;

`a^(4x)=a^1`

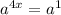
4x = 1

Divide both-side by 4

`x=(1)/(4)`

`\text{Log}_aa=4((1)/(4))`
`\text{Log}_aa=1`