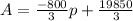Question

A local water park found that if the price of admission was $19, the attendance was about 1550 customers per week. When the price of admission was dropped to $16,attendance increased to about 2350 per week. Write a linear equation for the attendance in terms of the price,p. (A = mp + b)

Answer 1

Given:

When the price of admission was $19, the attendance was about 1550 customers per week

And, when the price of admission was dropped to $16,

attendance increased to about 2350 per week

Let the attendance = A

And the price = p

The linear equation will be A = mp + b

Where (m) is the slope and (b) is the y-intercept

So,

When p = 19, A = 1550

When p = 16, A = 2350

So,

`m=(2350-1550)/(16-19)=(800)/(-3)=-(800)/(3)`

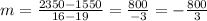
So,

`A=-(800)/(3)p+b`

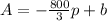
we will find the value of (b) as follows:

`\begin{gathered} 1550=-(800)/(3)\cdot19+b \\ 1550=-(15200)/(3)+b \\ b=(19850)/(3) \end{gathered}`

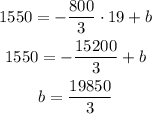
So, the answer will be the linear equation is:

`A=(-800)/(3)p+(19850)/(3)`