Question

What is the length of the hypotenuse of the right triangle with coordinates:(-2, -1), (-6,5), and (4, 3)?

Answer 1

10.2 units

Explanation:

The first thing is to make a sketch of the triangle formed in the Cartesian plane, like this:

The hypotenuse is the side opposite the right angle, therefore, it would be the side from the point (-6, 5) to the point (4, 3).

We calculate the distance between these two points using the following formula:

`d=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

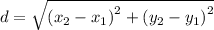
We replace and calculate the length of the hypotenuse:

`\begin{gathered} d=√(\left(4-\left(-6\right)\right)^2+\left(3-5\right)^2) \\ d=\sqrt[]{(4+6)^2+(3-5)^2} \\ d=\sqrt[]{(10)^2+(-2)^2} \\ d=\sqrt[]{100+4} \\ d=\sqrt[]{104} \\ d\cong10.2 \end{gathered}`

The length of the hypotenuse is 10.2 units.