Question

Graph the system of linear inequalities.x + 2y ≥ 2-x + y ≤ 0

Answer 1

INFORMATION:

We have the next system of equations

`\begin{gathered} x+2y\ge2 \\ -x+y\leq0 \end{gathered}`

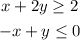
And we must graph it

STEP BY STEP EXPLANATION:

To graph the system, we need to graph first the two inequalities as equations. So, we would have

`\begin{gathered} x+2y=2 \\ -x+y=0 \end{gathered}`

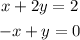
- x + 2y = 2:

To graph it, we can find the x and y intercepts.

x intercept:

To find it, we need to replace y = 0, and solve for x

`\begin{gathered} x+2(0)=2 \\ x=2 \end{gathered}`

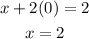
y intercept:

To find it, we need to replace x = 0, and solve for y

`\begin{gathered} 0+2y=2 \\ y=1 \end{gathered}`

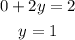
So, the graph would be a line that passes through the points (2, 0) and (0, 1).

Since the symbol of this inequality is ≥, the graph would be the values that are on the line and above it.

- -x + y = 0:

To graph it, we can rewrite the equation as

`y=x`

And this is the identity line.

So, since the symbol of this inequality is ≤, the graph would be the identity line and the values below it.

Finally, the graph of the system would be the common part of the graph of each inequality

So, the graph of the system is the part colored in red and blue at the same time

ANSWER: