ANSWER

Step-by-step explanation
We have that the restaurant needs at least 261 forks.
There are currently 205 forks.
First, we have to find the number of forks that the restaurant currently needs.
We do that by finding the difference between the number of forks they have from the number of forks they need:
261 - 205 = 56 forks
They need at least 56 forks.
We have that each set of forks on sale has 10 forks each.
Let the number of sets they need be x.
This means that the amount of forks they should buy must be greater than or equal to 56. That is:
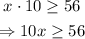
That is the inequality that can be used to determine the minimum number of sets of forks Grayson should buy.