Question

IQ is normally distributed with a mean of 100 and a standard deviation of 15.a) Suppose one individual is randomly chosen. Find the probability that this person has an IQ greater than 95.Write your answer in percent form. Round to the nearest tenth of a percent.P(10 greater than 95) =%b) Suppose one individual is randomly chosen. Find the probability that this person has an IQ less than 125.Write your answer in percent form. Round to the nearest tenth of a percent.P(IQ less than 125) =%c) In a sample of 800 people, how many people would have an IQ less than 110?peopled) In a sample of 800 people, how many people would have an IQ greater than 140?peopleCheck Answer

Answer 1

To answer this questions we need to remember the standard score formula given by:

`z=(x-\mu)/(\sigma)`

where x is the value we are looking for, mu si the mean and sigma is the standard deviation.

a.

We need the probability:

`P(IQ>95)`

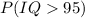
using the standard score this is equivalent to:

`\begin{gathered} P(IQ>95)=P(z>(95-100)/(15)) \\ =P(z>-0.3333) \end{gathered}`

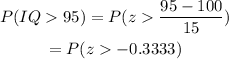
Using a normal distribution table we have:

`P(z>-0.3333)=0.6306`

Therefore the probability to select a person with more than 95 IQ points is 63.1%.

b.

Following the same reasoning as before we have:

`\begin{gathered} P(IQ<125)=P(z<(125-100)/(15)) \\ =P(z<1.6667) \\ =0.9522 \end{gathered}`

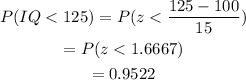
Therefore the probability to select a person with less than 125 IQ points is 95.2%

c.

To find how many people of this sample have more less than 110 points we need to find that probability:

`\begin{gathered} P(IQ<110)=P(z<(100-110)/(15)) \\ =P(z<-0.666) \\ =0.7475 \end{gathered}`

Multiplying this value with the sample size we have

`(800)(0.7475)=598`

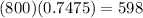
Therefore 598 people will have an IQ less than 110.

d.

By the same reasoning as before we have:

`\begin{gathered} P(IQ>140)=P(z>(140-100)/(15)) \\ =P(z>2.6667) \\ =0.0038 \end{gathered}`

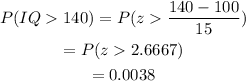
Multiplying this value with the sample size we have

`(800)(0.0038)=3`

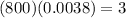
Therefore 3 people will have an IQ greater than 140.