Question

Use the drawing tool(s) to form the correct answer on the provided graph.

Graph the solution to this system of inequalities in the coordinate plane.
3y>2x + 122x + y ≤ -5Having trouble rewriting in form. Graphing once in form okay.

Answer 1

Explanation

We are given the following system of inequalities:

`\begin{gathered} 3y>2x+12 \\ 2x+y\leqslant-5 \end{gathered}`

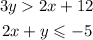
We are required to graph the given system of inequalities.

This is achieved thus:

- First, we determine two coordinates from the given inequalities:

`\begin{gathered} 3y>2x+12 \\ \text{ Suppose }3y=2x+12 \\ \text{ Let x = 0} \\ 3y=12 \\ y=4 \\ Coordinate:(0,4) \\ \\ \text{Suppose }3y=2x+12 \\ \text{ Let y = 0} \\ 0=2x+12 \\ 2x=-12 \\ x=-6 \\ Coordinate:(-6,0) \end{gathered}`

- Now, we plot the points on a graph. Since the inequality is "strictly greater than", the line drawn will be broken. The graph is shown below:

- Using the second inequality, we have:

`\begin{gathered} 2x+y\leqslant-5 \\ \text{ Suppose }2x+y=-5 \\ \text{ Let y = 0} \\ 2x=-5 \\ x=-2.5 \\ Coordinate:(-2.5,0) \\ \\ \text{Suppose }2x+y=-5 \\ \text{ Let x = 0} \\ y=-5 \\ Coordinate:(0,-5) \end{gathered}`

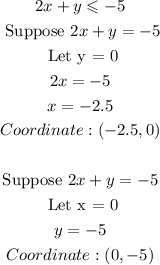
The graph becomes:

Combining both graphs, we have the solution to be:

The solution is the intersection of both graphs as indicated above.