Question

Two weather stations are aware of a thunderstorm located at point C. The weather stations A and B are 24 miles apart.

Answer 1

Assuming the dashed lines are parallel and perpendicular to the base, we can start by draw a third parallel line that passes through C and naming some distances:

Now, we can see that the given angles are alternate interior angles with respect to the angles formed by the new perpendicular line and the lines AC and BC:

Now, we can see that b and the base a + 24 are related with the tangent of 48°:

`\tan 48\degree=(a+24)/(b)`

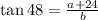
Also, b and a are related with the tangent of 17°:

`\tan 17\degree=(a)/(b)`

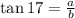
We can solve both for b and equalize them:

`\begin{gathered} b=(a+24)/(\tan48\degree) \\ b=(a)/(\tan17\degree) \\ (a+24)/(\tan48°)=(a)/(\tan17\degree) \\ a\tan 17\degree+24\tan 17\degree=a\tan 48\degree \\ a\tan 48\degree-a\tan 17\degree=24\tan 17\degree \\ a(\tan 48\degree-\tan 17\degree)=24\tan 17\degree \\ a=(24\tan17\degree)/(\tan48\degree-\tan17\degree)=(24\cdot0.3057\ldots)/(1.1106\ldots-0.3057\ldots)=(7.3375\ldots)/(0.8048\ldots)=9.1162\ldots \end{gathered}`

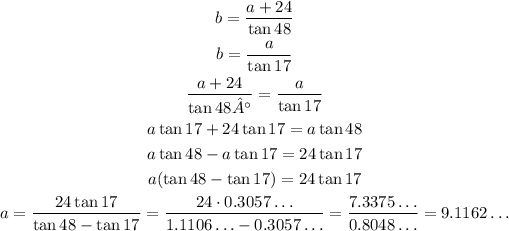
Now, we can relate a and x with the sine of 17°:

`\begin{gathered} \sin 17\degree=(a)/(x) \\ x=(a)/(\sin17\degree)=(9.1162\ldots)/(0.2923\ldots)=31.18\ldots\approx31.2 \end{gathered}`

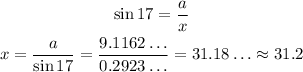
And x is the distance between A and C, the storm. Thus the answer is approximately 31.2 miles, fourth alternative.