We have a parallelogram.
The diagonals of a parallelogram bisect each other. This means that each diagonal is divided in two equal segments by the other diagonal.
This let us write:
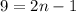
and
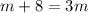
We can solve for n as:
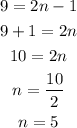
and for m as:
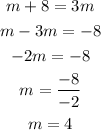
Answer: the value of m is 4.