ANSWER:
c. 133°
Explanation:
We have that there is a chord that divides the circle in two equal parts because it passes through the middle of the circle. Since it is half of the circle, the arc is 180°, we can see that this arc is the sum of the angles a + b, this angle must measure half of 180°, therefore:

Now the angle c° must measure half of the 86° arc, therefore:
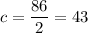
That means that a° + b° + c° is equal to:

Therefore, the correct answer is c. 133°