Question

A motorboat takes 5 hours to travel 200 miles going upstream. The return trip takes 4 hours going downstream. What is the rate of the boat in still water and what is the rate of the current? Rate of the boat still in water=Rate of the current=

Answer 1

Given,

Time taken by motorboat to going 200 miles upstream is 5 hours.

Time taken by motorboat to going 200 miles downstream is 4 hours.

At upstream,

The speed of boat is offosed by the speed of current.

At downstream,

The speed of boat is incraesed by the speed of current.

Consider,

The speed of boat is b.

The speed of current is c.

The speed is calculated as,

`\begin{gathered} \text{Speed=}(dis\tan ce)/(time) \\ b-c=(200)/(5) \\ b-c=40 \\ b=c+40\ldots\text{.}\mathrm{}(1) \end{gathered}`

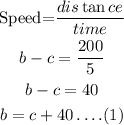
Similarly,

`\begin{gathered} \text{Speed=}(dis\tan ce)/(time) \\ b+c=(200)/(4) \\ b+c=50 \\ b=50-c\ldots\text{.}(2) \end{gathered}`

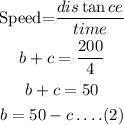
Substituting the value of b from equation (2) then,

`\begin{gathered} c+40=50-c \\ 2c=10 \\ c=5\text{ mile per hour} \end{gathered}`

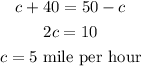
Substituting the value of c in equation (1) then,

`\begin{gathered} b=5+40 \\ b=45\text{ mile per hour} \end{gathered}`

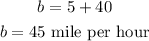
Hence, the speed of boat is 45 mile per hour and speed of current is 5 mile per hour.