Question

Determine the equation of the line that passes through the point (1/−3,−9) and is perpendicular to the line 5y+x=1.

Answer 1

Given the following equation of a line:

`5y+x=1`

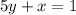
We will write the equation in the slope-intercept form: y = m x + b

`\begin{gathered} 5y+x=1 \\ 5y=-x+1 \\ \\ y=-(1)/(5)x+(1)/(5) \end{gathered}`

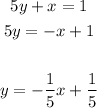
Now, we will find the equation of the line that is perpendicular to the given line.

Note: if the slope of the given line = m

So, the slope of the perpendicular line = -1/m

From the given line: slope = m = -1/5

So, the slope of the perpendicular line = -1/m = 5

The required line passes through the point (-1/3, -9)

We will use the point-slope form to write the equation of the required line:

`\begin{gathered} (y-k)=m*(x-h) \\ \\ y-(-9)=5*(x-(-(1)/(3))) \\ \\ y+9=5x+(5)/(3) \end{gathered}`

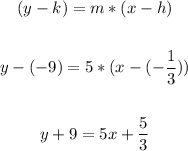
Simplify the equation to be like the standard equation:

`\begin{gathered} y+9=5x+(5)/(3)\to*3 \\ 3y+27=15x+5 \\ \\ 3y-15x=-22 \end{gathered}`

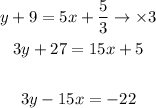
So, the answer will be:

3y - 15x = -22