Solution:

Step 1:
Factor out the common term
The common term is 3x
By doing this, we will have
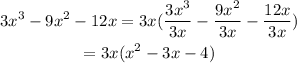
Step 2:
Factorise the quadratic expression in the bracket

By doing this, we will have to look for two factors to multiply to give i4 and if we add them together, we will have -3
The two factors are -4 and +1
therefore,
Replace -3x with -4x + x
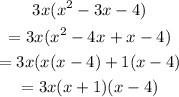
Hence,
The final answer is = (x-4)