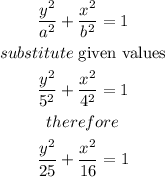Question

An ellipse has vertices (0,-5) and (0,5) and a minor axis of length 8.Part I: In what direction is this ellipse oriented? Part II: What are the coordinates of the center of this ellipse? Part III: What are the values of a and b for this ellipse? Part IV: Write the equation of this ellipse.

Answer 1

we know that

vertices (0,-5) and (0,5) --------> is a vertical ellipse

the minor axis of length 8 ------> 2b=8 -------> b=4

so

Part I: In what direction is this ellipse oriented?

Is a vertical ellipse

Part II: What are the coordinates of the center of this ellipse?

The center of the ellipse is the midpoint between the vertices

The midpoint between (0,-5) and (0,5) is the origin (0,0)

The center is the point (0,0)

Part III: What are the values of a and b for this ellipse?

b=4

2a=10 ---------> a=5

Part IV: Write the equation of this ellipse.

`\begin{gathered} (y^2)/(a^2)+(x^2)/(b^2)=1 \\ substitute\text{ given values} \\ (y^2)/(5^2)+(x^2)/(4^2)=1 \\ therefore \\ (y^2)/(25)+(x^2)/(16)=1 \end{gathered}`