Question

A metallurgist has One alloy containing 49% copper and another containing 62% copper. How many pounds of each alloy must he used to make 51 pounds of a third alloy containing 56% copper?

Answer 1

Step-by-step explanation

Step 1

a)

Let

x represents the pounds of the 49 % copper alloy

y represents the pounds of the 62 % copper alloy

then,

if we want to make a 51 pounds of a new alloy,

`x+y=51\rightarrow equation(1)`

b)this new allo contains 56% of copper , so

total of cooper = pounds of alloy * percentage

`\begin{gathered} 0.49x+0.62y=51\cdot0.56 \\ 0.49x+0.62y=28.56\rightarrow equation\text{ (2)} \end{gathered}`

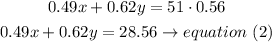
Step 2

Solve the equations

a) isolate x in equation (1) and replace in equation(2)

`\begin{gathered} x+y=51\rightarrow equation(1) \\ \text{subtract y on both sides} \\ x+y-y=51-y \\ x=51-y\rightarrow equation(3) \end{gathered}`

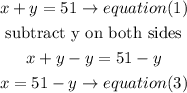
Now, replace in equation (2)

`\begin{gathered} 0.49x+0.62y=28.56\rightarrow equation\text{ (2)} \\ 0.49(51-y)+0.62y=28.56 \\ 24.99-0.49y+0.62y=28.56 \\ \text{add like terms } \\ 24.99+0.13y=28.56 \\ \text{subtract 24.99 on both sides} \\ 24.99+0.13y-24.99=28.56-24.99 \\ 0.13y=3.57 \\ \text{divide both sides by 0.13} \\ (0.13y)/(0.13)=(3.57)/(0.13) \\ y=27.46 \\ \end{gathered}`

now, replace the y value into equation (3) to get x

`\begin{gathered} x=51-y\rightarrow equation(3) \\ x=51-y \\ x=51-27.46 \\ x=23.54 \\ \end{gathered}`

therefore, the answer is

23.54 lb of the 49% copper alloy

27.46 lb of the 62% copper alloy