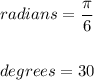Question

a. in radiansb.in degreesHint:HEARRERANote: You can earn partial credit on this problem.Preview My AnswersSubmit Answers

Answer 1

EXPLANATIONS:

Given;

We are given the following expression;

`arctan((1)/(√(3)))`

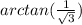
Required;

We are required to find the angle measure of this in both radians, and degrees.

Step-by-step solution;

For the angle whose tangent is given as 1 over square root of 3, on the unit circle, we would have

`\begin{gathered} tan\theta=(1)/(√(3)) \\ Rationalize: \\ \\ (1)/(√(3))*(√(3))/(√(3)) \\ \\ =(√(3))/(√(3)*√(3)) \\ \\ =(√(3))/(3) \end{gathered}`

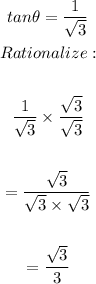
On the unit circle, the general solution for this value as shown would be;

`tan^(-1)((√(3))/(3))=(\pi)/(6)`

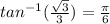
To convert this to degree measure, we will use the following equation;

`(r)/(\pi)=(d)/(180)`

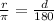
We now substitute for the value of r;

`\begin{gathered} ((\pi)/(6))/(\pi)=(d)/(180) \\ \\ (\pi)/(6)/(\pi)/(1)=(d)/(180) \\ \\ (\pi)/(6)*(1)/(\pi)=(d)/(180) \\ \\ (1)/(6)=(d)/(180) \end{gathered}`

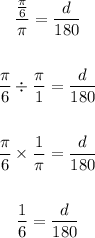
We now cross multiply;

`\begin{gathered} (180)/(6)=d \\ \\ 30=d \end{gathered}`

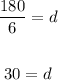
Therefore;

ANSWER:

`\begin{gathered} radians=(\pi)/(6) \\ \\ degrees=30\degree \end{gathered}`