Question

In 2 years, Ariel wants to buy a bicycle that costs 1,000.00. If she opens a savings account that earns 9%interest compounded quarterly, how much will she have to deposit as principal to have enough money in 2 years to buy the bike?

Answer 1

Let's first list down the information given in the scenario:

a.) In 2 years ariel wants to buy a bicycle that costs 1,000.00

b.) She opens a savings account that earns 9% interest compounded quarterly

Question: How much will she have to deposit as principal to have enough money in 2 years to buy the bike?

To be able to determine the principal amount Ariel will need to deposit, let's use this formula for Compound Interest:

`\text{ A = }P(1\text{ + }((r)/(n))/(100))^(nt)`

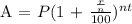
Where:

A = Is the final amount/ cost of the bicycle = 1,000

n = Number of times the interest is being compounded = 4

r = Interest rate = 9%

t = No. of periods elapsed/ No. years the principal money be deposited

P = Principal amount/ amount to be deposited

Let's now find the principal amount:

`\text{ A = }P(1\text{ + }((4)/(n))/(100))^(nt)\text{ }\rightarrow\text{ 1,000 = }P(1\text{ + }((9)/(4))/(100))^(4(2))`
`\text{1,000 = }P(1\text{ + }(2.25)/(100))^8\text{ }\rightarrow\text{ 1,000 = }P(1\text{ + }0.0225)^8\text{ }\rightarrow1,000=P(1.0225)^8`
`\text{ P = }(1,000)/((1.0225)^8)\rightarrow\text{ P = }(1,000)/(1.19483114181)`
`\text{ P = 836.93835 }\cong\text{ 836.94}`

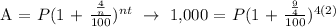
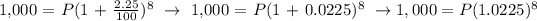
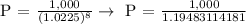
Therefore, Ariel must deposit a principal amount of 836.94 for her to be able to buy the bike in 2 years.