Question

Fidn the x intercept(s) and the coordinates of the vertex for the parabola y=x^2-8x+12 if there is more then one x intercept esperate them with commas!

Answer 1

`y=x^2-8x+12`

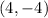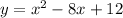
To calculate the x-intercepts we replace y=0 and solve for x

`x^2-8x+12=0`

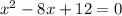
where a is 1, b is -8 and c 12

so factor the expression using

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

replacing

`\begin{gathered} x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(1)(12)^{}}}{2(1)} \\ \\ x=\frac{8\pm\sqrt[]{64-48}}{2} \\ \\ x=\frac{8\pm\sqrt[]{16}}{2} \\ \\ x=(8\pm4)/(2) \\ \\ x=4\pm2 \end{gathered}`

so x have two solutions because there are two x-intercepts

`\begin{gathered} x_1=4+2=6 \\ x_2=4-2=2 \end{gathered}`

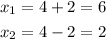
then the x-intercepts are 6 and 2, the corrdinates are

`\begin{gathered} (6,0) \\ (2,0) \end{gathered}`

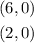
Vertex

the vertex is a point (x,y) to calculate x we use

`x=(-b)/(2a)`

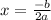
and replace

`\begin{gathered} x=(-(-8))/(2(1)) \\ \\ x=(8)/(2)=4 \end{gathered}`

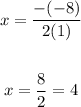
now replace x=4 on the equation of the parable to find y

`\begin{gathered} y=x^2-8x+12 \\ y=(4)^2-8(4)+12 \\ y=16-32+12 \\ y=-4 \end{gathered}`

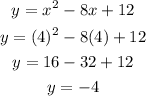
the coordinate of the vertex is

`(4,-4)`