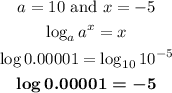Part a)
For this part, we can use the following properties:

So, applying the above property of exponents, we have:
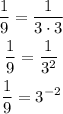
Now, applying the above property of logarithms, we have:
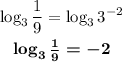
Part b)
For this part, we can apply the following property of logarithms:
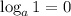
Then, in this case, we have:
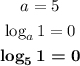
Part c)
For this part, we can apply the following property of logarithms:
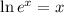
So, we have:
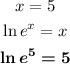
Part d)
For this part, we can rewrite 0.00001 like this:
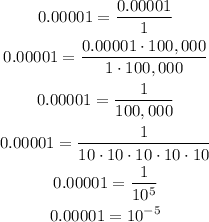
Now, applying the above property of logarithms, we have: