The formula for calculating the amount remaining after a number of half years , n is :
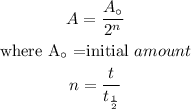
The lab store mass of Cesium-137 is 30mg in 1975
then the mass of Cesium-137 in 2065,
Time period =2065-1975
time period t=90 years,
substitute the value and solve for A
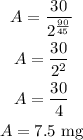
In 2065, the mass of Cesium -137 will be 7.5 mg
Answer : 7.5mg