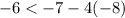Question

Which of the following values are solutions to the inequality -6<-7-4x?1. 12. -83. 5or none

Answer 1

The Solution:

Given:

Required:

Find f(2):

`\begin{gathered} f(2)=√([(-5*2)+14])=√(-10+14)=√(4)=2 \\ \\ f(2)=2 \end{gathered}`

Find g(-5):

`\begin{gathered} g(-5)=(-5)/((-5)^2-7)=(-5)/(25-7)=-(5)/(18) \\ \\ g(-5)=-(5)/(18) \end{gathered}`

Find h(-1/2):

`\begin{gathered} h(-(1)/(2))=|6(-(1)/(2))|-9=|-3|-9=3-9=-6 \\ \\ h(-(1)/(2))=-6 \end{gathered}`

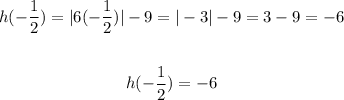
Answer:

f(2) =

`-6<-7-4x`

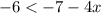
now we can solve the inequalty for x by passing the -7 to the other side:

`\begin{gathered} 7-6<-4x \\ 1<-4x \end{gathered}`

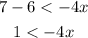
Now to change the sign of the -4x we have to invert the inequality:

`\begin{gathered} -1>4x \\ (-1)/(4)>x \end{gathered}`

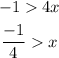
so the only solution is -8 and we can prove it:

`-6<-7-4(-8)`