Question

How do u know if an equation has rational, irrational or complex solution

Answer 1

We have the equation:

`49a^2-16=0`

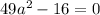
We can factorize this equation as:

`\begin{gathered} 49a^2-16=0 \\ (7a)^2-4^2=0 \\ (7a-4)(7a+4)=0 \end{gathered}`
`\begin{gathered} 7a-4=0\longrightarrow a_1=(4)/(7) \\ 7a+4=0\longrightarrow a_2=-(4)/(7) \end{gathered}`

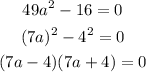
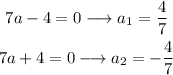
In this case, we have 2 rational solutions.

If the solution implies the square root of -1, then we would have 2 complex solutions.

If the solution implies a square root that does not have a rational solution, then we have 2 irrational solutions.

We can see it when we apply the quadratic formula:

`x=-(b)/(2a)\pm\frac{\sqrt[]{b^2-4ac}}{2a}`

The term with the square root defines what type of solution we have:

If b^2-4ac<0, then we have complex solutions.

If the square root of b^2-4ac does not have a rational solution (b^2-4ac is not a perfect square), then we have irrational solutions.

If b^2-4ac is a perfect square (its square root have a rational solution), we will have rational solutions.