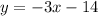Question

A line segment, ST, has endpoints S(-7,-3) and T(-1,-1). Which of the following equations represents the perpendicular bisector of the line segment? A. y = 2x - 15 B. y = -3x - 14 C. y = 6x - 14 D. y = -3x - 20

Answer 1

The given points are: (-7,-3) and (-1,-1)

The slope of the line segment is:

`\begin{gathered} m=(-1-(-3))/(-1-(-7)) \\ m=(-1+3)/(-1+7) \\ m=(2)/(6) \\ m=(1)/(3) \end{gathered}`

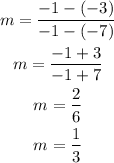
Recall that the product if solpes of perpendicular line give -1.

The the slope of the perpendicula bisector is:

`\begin{gathered} m_1=(1)/((1)/(3)) \\ m=3 \end{gathered}`

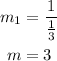
Therefore the slope of the perpendicular bisector is -3.

Recall that the perpendicular bisector passes through the center of a line segment.

Hence the perpendicular bisector will pass through:

`\begin{gathered} ((-7-1)/(2),(-3-1)/(2)) \\ =((-8)/(2),(-4)/(2)) \\ =(-4,-2) \end{gathered}`

Using the point slope form, the equation of the perpendicular bisector is:

`\begin{gathered} y-(-2)=-3(x-(-4)) \\ y+2=-3x-12 \\ y=-3x-12-2 \\ y=-3x-14 \end{gathered}`

Therefore the required equation is:

`y=-3x-14`