Question

Triangle UVW, with vertices U(-6,2), V(-4,6), and W(-8,5), is drawn inside arectangle, as shown below.What is the area, in square units, of triangle UVW?

Answer 1

Okay, here we have this:

Considering the provided vertices, we are going to calculate the requested area, so we obtain the following:

Then we will first calculate the measure of each side and later with Heron's formula we will find the area, then we have:

`\begin{gathered} u=√(((-4-(-8))^2+(6-5)^2)) \\ u=√(4^2+1^2) \\ u=√(17) \end{gathered}`
`\begin{gathered} w=√((-6-(-4))^2+(2-6)^2) \\ w=√(2^2+(-4)^2) \\ w=√(20) \end{gathered}`
`\begin{gathered} v=√((-6-(-8))^2+(2-5)^2) \\ v=√(2^2+(-3)^2) \\ v=√(13) \end{gathered}`

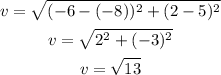
Then, the area is:

Finally we obtain that the triangle's area is equal to 7 square units.