Solution
- In order to plot these vectors using Parallelogram law, we need to write them in rectangular form i.e. in terms of the x and y-components.
- This is done below:
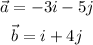
- We can then proceed to plot the vectors on a graph.
- For vector a, the line of magnitude extends from the origin (0, 0) to the point (-3, -5) while the line of the magnitude of vector b extends from the origin (0, 0) to the point (1, 4).
- This is shown below:
- The vector addition of both vectors is given below:
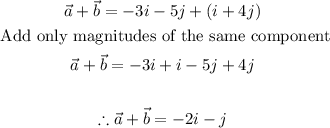
- This implies that the vector addition of both vectors extends from the origin (0,0) to the point (-2, -1)
- This is depicted below: