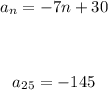Question

Write an equation for the n th term of the arithmetic sequence 23, 16, 9, 2, ... .Then find a25?

Answer 1

Given the sequence:

23, 16, 9, 2

Use the arithmetic sequence formula:

`a_n=a_1+(n-1)d`

Where

an = nth term

a1 = first term

n = number of terms

d = common difference

d = a2 - a1 = 16-23 = -7

Since d = -7, let's find the equation for the nth term.

`\begin{gathered} a_n=23+(n-1)-7 \\ a_n=23+n(-7)-1(-7) \\ a_n=23-7n+7 \\ \text{Combine like terms} \\ a_n=-7n\text{ +23}+7 \\ \\ a_n=-7n+30 \end{gathered}`

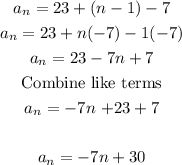
The equation for the nth term is:

`a_n=-7n+30`

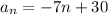
Let's find the 25th term, a25:

Substitute n for 25 and evaluate

`\begin{gathered} a_(25)=-7(25)+20 \\ \\ a_(25)=-175+30 \\ \\ a_(25)=-145 \end{gathered}`

ANSWER:

`\begin{gathered} a_n=-7n+30 \\ \\ \\ a_(25)=-145 \end{gathered}`