Question

A 1,470.39 N rocket travels at constant speed for 1,522.64m in 2.11 seconds. What is the kinetic energy of the rocket?

Answer 1

Given data:

* The weight of the rocket is 1470.39 N.

* The distance traveled by the rocket is 1522.64 m.

* The time taken by the rocket is 2.11 seconds.

Solution:

The velocity of the rocket in terms of the distance and time is,

`\begin{gathered} v=\frac{\text{distance}}{\text{time}} \\ v=(1522.64)/(2.11) \\ v=721.63\text{ m/s} \end{gathered}`

The mass of the rocket from the weight is,

`\begin{gathered} mg=1470.39 \\ m=(1470.39)/(g) \end{gathered}`

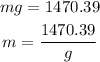
where g is the acceleration due to gravity,

Substituting the known values,

`\begin{gathered} m=(1470.39)/(9.8) \\ m=150.04\text{ kg} \end{gathered}`

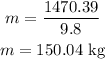
The kinetic energy of the rocket in terms of mass and velocity of the rocket is,

`\begin{gathered} K=(1)/(2)mv^2 \\ K=(1)/(2)*150.04*721.63^2 \\ K=39066654.26\text{ J} \\ K=39.07*10^6\text{ J} \\ K=39.07\text{ MJ} \end{gathered}`

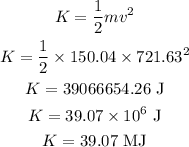
Thus, the kinetic energy of the rocket is 39.07 MJ.