Answer:
Table 3
Explanation:
A linear function has a constant slope.
To determine if the table represents a linear function, find the slope for two different pairs of points.
Table 1
Using the points (1,-2), (2,-6)
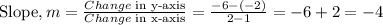
Using the points (2,-6), (3,-2)
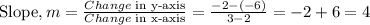
The slopes are not the same, thus, the function is not linear.
Table 3
Using the points (1,-2), (2,-10)
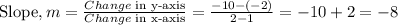
Using the points (2,-10), (3,-18)

The slopes are the same, thus, the function is linear.
Table 3 is the correct option.