We are given the following information:
Weight of skater 1 = 625 N
Weight of skater 2 = 725 N
Final velocity of skater 2 = 1.5 m/s
Final velocity of skater 1 = ?
Recall from the law of conservation of momentum, the total momentum before the collision and after the collision must be equal.
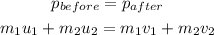
The initial velocities of both skaters are 0 m/s
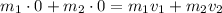
Also, m = W/g
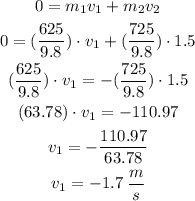
So, the lighter skater will travel with a velocity of 1.7 m/s
The negative sign means that the lighter skater will be traveling oppositely to the heavier skater.