The triangle midpoint theorem is as stated above.
In our case,
RS is joining the midpoints of NP and PQ.
Hence by the triangle midpoint theorem,
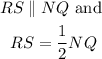
Therefore,
triangle PRS is similar to triangle PNQ.
This means that the ratios of their corresponding sides are equal.
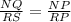
Since R is the midpoint of NP then
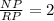
Therefore,

Hence,
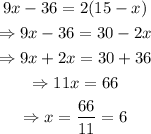
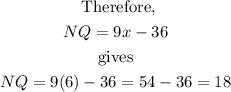
Hence the measure of NQ is 18