We have a system of equation problem
x= cost of almonds per pound
y= cost of the jelly beans per pound
For the first equation, we have
3 pounds of almonds
8 pounds of jelly beans
total $34
so the equation is
3x+8y=34
For the second equation we have
5 pounds of almonds
2 pounds of jelly beans
total $17
so the equation is
5x+2y=17
so our system of equation is
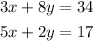
In order to solve the system we will multiply the second equation by -4
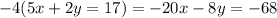
then we sum the equation above with the first equation

then we sum similar terms and isolate the x to find the value of x
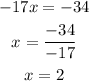
then we substitute the value of x=2 in the first equation and we find the value of y
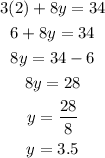
The solution is
x= $ 2 cost of each pound of almond
y= $3.50 cost of each pound of jelly beans