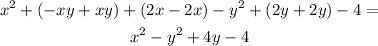Question

I need help solving questions 28 and 34 by expanding and simplifying please

Answer 1

#28

The given expression is

`\lbrack x+(y-2)\rbrack\lbrack x-(y-2)\rbrack`

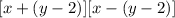
At first, we will simplify each square bracket

Note that, the + sign does not change the terms in the bracket but the - sign change the signs of the terms inside the bracket

`\begin{gathered} \lbrack x+(y-2)\rbrack=\lbrack x+y-2\rbrack \\ \lbrack x-(y-2)\rbrack=\lbrack x-y+2\rbrack \end{gathered}`

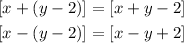
Now, we will multiply the 2 brackets

`\begin{gathered} \lbrack x+y-2\rbrack\lbrack x-y+2\rbrack= \\ (x)(x)+(x)(-y)+(x)(2)+(y)(x)+(y)(-y)+(y)(2)+(-2)(x)+(-2)(-y)+(-2)(2)= \\ x^2-xy+2x+xy-y^2+2y-2x+2y-4 \end{gathered}`

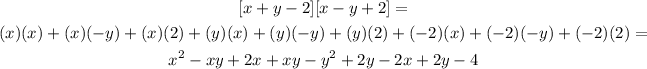
Now we will add the like terms

`\begin{gathered} x^2+(-xy+xy)+(2x-2x)-y^2+(2y+2y)-4= \\ x^2-y^2+4y-4 \end{gathered}`