Question

What is the factorization of the trinomial below?x^3 - 2x² - 35x

Answer 1

Notice that the factor x is a common factor for all three terms. Then, factor out x:

`x^3-2x^2-35x=x(x^2-2x-35)`

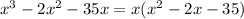
Notice that the factor x²-2x-35 is a quadratic expression.

Find two numbers whose sum is -2 and whose product is -35 to factor out the quadratic expression. Since 5-7 = -2 and (5)(-7)=-35, those two numbers are -7 and 5. Then, the quadratic expression can be factored out as:

`x^2-2x-35=(x-7)(x+5)`

Then:

`x(x^2-2x-35)=x(x-7)(x+5)`

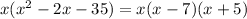
Then, the factorization of the given trinomial is:

`x^3-2x^2-35x=x(x-7)(x+5)`

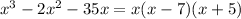
Therefore, the correct choice is option C) x(x-7)(x+5)