Question

There are as many even counting numbers as there are counting numbers. Is this true or false?

Answer 1

The sets of even and odd counting numbers are both infinite in size (number of elements). However, we can map each even counting number to each odd counting number as follows:

`\begin{gathered} 2\rightarrow1 \\ 4\rightarrow3 \\ 6\rightarrow5 \\ 8\rightarrow7 \\ \text{And so on}\ldots \end{gathered}`

So we have the mapping rule:

`\begin{gathered} 2n\rightarrow2n-1 \\ \text{Where }n=1,2,3,\ldots \end{gathered}`

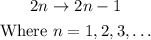
Then, we can say that there are as many even counting numbers as there are counting numbers, or equivalently, that both sets have the same cardinality.

Answer: True