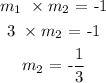Answer:
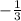
Step-by-step explanation:
Here, we want to get the gradient of the line L3
The equation of a straight line can be expressed as:
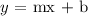
where m is the gradient (slope) and b is the y-intercept (the y-value when x = 0)
Now,let us write the equation of the first line in the slope-intercept form
Mathematically, we have this as:
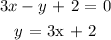
The gradient of the first line is 3
Now,let us get the gradient of the second line L3
Mathematically, when two lines ae perpendicular, the product of their gradients (slopes) equal -1
Thus, we have it that: