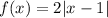Question

F(x)=2|x-1| Graph using transformations and describe the transformations of the parent function y =x^2.

Answer 1

[Please see that in the question should be a mistake regarding the parent function. It should be written y = |x| instead of y = x².]

To answer this question, we need to know that the below function is a transformation of the parent function, f(x) = |x|:

`f(x)=2|x-1|`

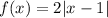
Describing the transformations

To end up with the above function from the parent function, we need to follow the next steps:

1. Translate the function, y = |x| one unit to right. We can do this by subtracting one unit to the parent function as follows:

`f(x)=|x-1|`

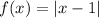
We can see this graphically as follows:

The blue function is the first transformation of the parent function, f(x) = |x|.

2. The function has been dilated by a factor of 2 from the x-axis. That is, the function has been dilated by a factor of 2 vertically. Then, we have:

`f(x)=2|x-1|`

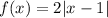
And now, we can see the transformation graphically as follows:

Therefore, the blue line is the graph representation of the function:

`f(x)=2|x-1|`