Question

If a plane covers a distance of 700 miles in 1 hour and 43 minutes, what is its speed?   A)   Give your answer in mph.   B)   Give your answer in ft/second

Answer 1

Given:

Distance covered by the plane, d = 700 miles

Time, t = 1 hour and 43 minutes.

Let's find the speed of the plane.

To find the speed, apply the formula:

`\text{Speed = }(dis\tan ce)/(time)`

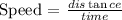
Where:

distance = 700 miles

time = 1 hour 43 minutes

(A) speed in mph.

mph is miles per hour.

Where:

60 minutes = 1 hour

Thus, to find the speed the time is to be in hours.

We have:

`t=1\frac{43\text{ minutes}}{60\text{ minutes}}=1(43)/(60)=1.716666\text{ hrs}\approx1.72\text{ hrs}`

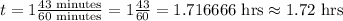
Thus, to find the speed in mph, we have:

`\text{Speed}=\frac{\text{distance}}{\text{time}}=(700)/(1.72)=407.8\text{ mph}`

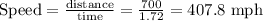
Therefore, the speed of the plane in mph is 407.8 mph

(B) To find the speed in ft/second

Let's first convert the distance from miles to feet

Where:

1 mile = 5280 feet

700 miles = 700 x 5280 = 3696000 feet

Also convert the time to seconds.

Where:

1 hour = 60 minutes x 60 seconds = 3600 seconds

1.7166 hours = 1.7166 x 3600 = 6180 seconds

Thus, we have:

Distance = 3696000 feet

Time = 6180 seconds

`\text{Speed = }\frac{dis\tan ce}{\text{time}}=(3696000)/(6180)=598.06\text{ ft/second}`

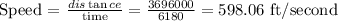
Therefore, the speed in ft/second is 598.06 ft/second

ANSWER:

(A) 407.8 mph

(B) 598.06 ft/second