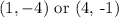Question

A number time 5 less that number has a product of -4. What are the two numbers?

Answer 1

Let the first number be x.

The second number is 5 times less than x => x - 5

Therefore, we can write the statement as

`\begin{gathered} x*(x-5)=-4 \\ x^2-5x=-4 \\ \therefore \\ x^2-5x+4=0 \end{gathered}`

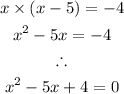
Solving the quadratic equation:

Let us replace -5x in the equation with -4x and -x to be able to factorize.

Hence,

`\begin{gathered} x^2-4x-x+4=0 \\ x(x-4)-1(x-4)=0 \\ (x-4)(x-1)=0 \\ \text{Therefore} \\ x-4=0\text{ } \\ or \\ x-1=0 \end{gathered}`

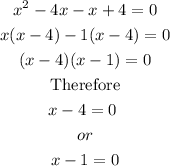
Hence,

`\begin{gathered} x=1 \\ or \\ x=4 \end{gathered}`

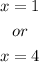
Therefore, the number can be 1 or 4.

The second number can be

`\begin{gathered} 1-5=-4 \\ or \\ 4-5=-1 \end{gathered}`

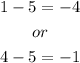
Therefore, the pair of numbers can be

`(1,-4)\text{ or (4, -1)}`