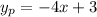Two perpendicular lines have reciprocal and opposite slopes.
First we have to write the given line in the slope-intercept form:

Where m is the slope and b is the y-intercept.
We have this equation:
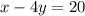
To write it in the slope-intercept form we have to clear y:
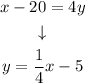
The slope is 1/4 and the y-intercept is -5.
The slope of the perpendicular line will be the opposite and reciprocal of 1/4, that's -4.
For now we have the perpendicular line's equation:
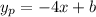
There are a lot of lines that are perpendicular to the given line, but only one that passes through (2, -5). We use this point to find the y-intercept by replacing x = 2 and y = -5 into the expression above and solving for b:
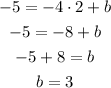
The y-intercept of the perpendicular line is 3.
The equation of a line perpendicular to the given line that passes through the point (2,-5) is