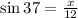Solution:
To find the appropiate trigonometric formula.
we know that,
for the right angle triangle, we have that,
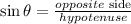
The side opposite to the right angle is hypotenuse, the side opposite to the angle theta is opposite side and the other side is adjacent side.
Also we have,
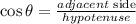
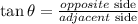
Using this we get,
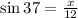
Answer is: